An introduction to chaotic dynamical systems devaney solutions – Delving into the enigmatic realm of chaotic dynamical systems, this exploration unveils the profound insights offered by Robert Devaney’s groundbreaking definition of chaos. Discover the captivating characteristics that distinguish chaotic systems from their non-chaotic counterparts, and embark on a journey through the practical applications and analytical methods that illuminate the complexities of these fascinating phenomena.
Introduction to Chaotic Dynamical Systems
Picture this: You flip a coin. Heads or tails? Simple, right? Not so fast. What if we told you that even this seemingly straightforward action could be a chaotic system? Chaotic dynamical systems are like mischievous puzzles that play with our expectations, revealing a hidden world of unpredictability amidst the mundane.
An introduction to chaotic dynamical systems devaney solutions will give you the tools to understand the complex behavior of systems that appear random. Like an information system’s sponsor and chief advocate , chaotic systems can be difficult to predict, but with the right knowledge, you can gain insights into their underlying patterns.
An introduction to chaotic dynamical systems devaney solutions will help you unlock the secrets of these fascinating systems.
Chaotic systems are found everywhere, from the weather to the stock market. They’re like unruly children who refuse to follow the rules, constantly surprising us with their erratic behavior. But don’t be fooled by their wild nature; these systems are governed by mathematical equations, and understanding them can unlock a treasure trove of applications in fields like cryptography, weather forecasting, and engineering.
An introduction to chaotic dynamical systems devaney solutions teaches us the intricate behaviors of complex systems. However, our current education system often fails to prepare us for the complexities of the real world. By embracing an ideal education system , we can empower individuals with the critical thinking and problem-solving skills needed to navigate the chaotic landscapes of the 21st century.
Ultimately, an understanding of chaotic dynamical systems devaney solutions can serve as a guiding principle for designing such an education system.
Devaney’s Definition of Chaos
In 1989, mathematician Robert Devaney came up with a definition of chaos that’s as clear as a bell. According to Devaney, a chaotic system must have three key ingredients:
- It must be sensitive to initial conditions, meaning even the tiniest change in the starting point can lead to wildly different outcomes.
- It must be topologically transitive, which means that any two points in the system can be connected by a continuous path.
- It must have dense periodic points, meaning that there are points that repeat themselves after a certain number of iterations.
If a system checks all these boxes, then it’s officially considered chaotic. And guess what? The coin flip we mentioned earlier? It actually fits the bill!
Buckle up, folks! If you’re into chaotic dynamical systems and Devaney’s solutions, you’re in for a treat. These systems can get as wild as an ideal mass spring system vibrating with simple . Just imagine, the springy antics of that system are a microcosm of the chaos that Devaney’s solutions can uncover.
So, let’s dive right in and explore the rollercoaster ride of chaotic dynamical systems.
Applications of Chaotic Dynamical Systems: An Introduction To Chaotic Dynamical Systems Devaney Solutions
Chaotic systems aren’t just theoretical curiosities; they have real-world applications that would make MacGyver jealous.
An introduction to chaotic dynamical systems devaney solutions presents a comprehensive overview of the subject. For those seeking a deeper understanding of the complexities of these systems, this book offers a valuable resource. But if you’re looking to streamline your business operations, consider implementing an erp system is . ERP systems can automate tasks, improve efficiency, and provide real-time insights into your business.
Returning to the topic at hand, an introduction to chaotic dynamical systems devaney solutions delves into the intricate nature of these systems, exploring their applications in various fields.
- Cryptography:Chaotic systems can create unbreakable codes that keep your secrets safe from prying eyes.
- Weather forecasting:Chaotic systems help us understand the unpredictable dance of the weather, giving us a heads-up on everything from hurricanes to heat waves.
- Engineering:Chaotic systems can help us design everything from better bridges to more efficient engines.
But hold your horses, partner! Using chaotic systems isn’t always a walk in the park. They can be unpredictable, and it’s hard to control their behavior. But that’s what makes them so darn exciting!
Delving into the complexities of chaotic dynamical systems as outlined by Devaney’s solutions, we encounter a curious parallel in the realm of biology. Just as these systems exhibit unpredictable yet intricate patterns, so too does the autonomic nervous system, an integral part of the autonomic nervous system , orchestrate our involuntary functions with a blend of chaos and order.
This connection between mathematical chaos and physiological regulation invites further exploration, hinting at deeper connections between seemingly disparate domains.
Methods for Analyzing Chaotic Dynamical Systems
Taming chaotic systems is no easy feat, but we’ve got some trusty tools to help us out:
- Lyapunov exponents:These numbers tell us how fast two nearby points in a chaotic system diverge. Positive exponents mean chaos!
- Strange attractors:These are geometric shapes that chaotic systems tend to hang out in. They’re like the wild west saloons of the mathematical world.
- Bifurcation diagrams:These graphs show how the behavior of a chaotic system changes as a parameter is varied. They’re like roadmaps for chaos!
With these tools in our arsenal, we can start to understand the enigmatic dance of chaotic systems.
Fractals and Chaotic Dynamical Systems
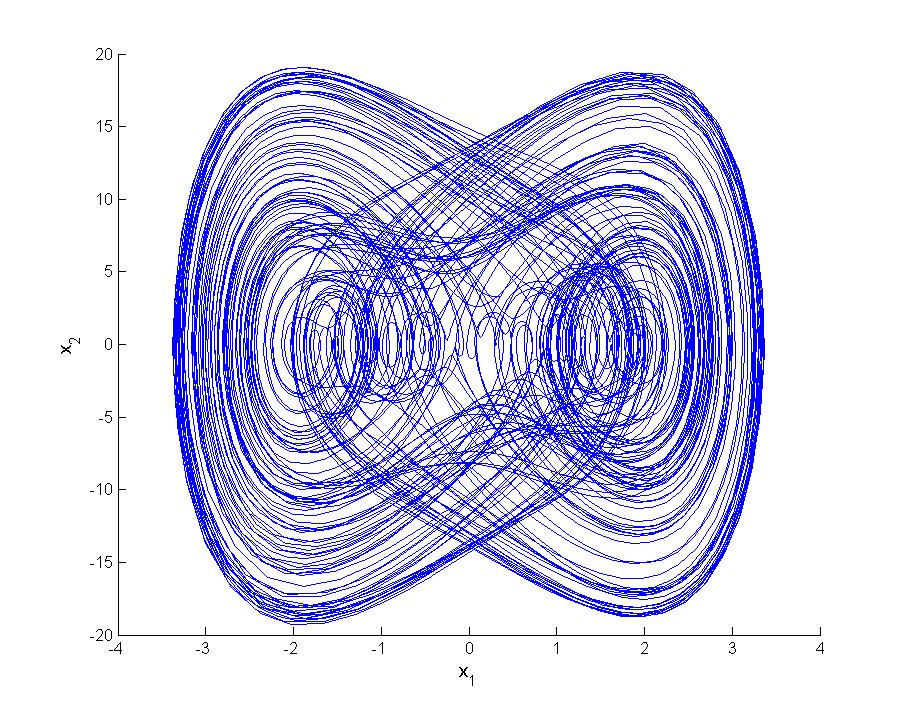
Fractals are like the fingerprints of chaos. They’re self-similar patterns that repeat themselves at different scales, creating intricate and often beautiful shapes.
An introduction to chaotic dynamical systems devaney solutions provides an understanding of complex systems. Just like an enterprise resource planning system is designed to integrate data and streamline processes, an introduction to chaotic dynamical systems devaney solutions offers a framework for comprehending unpredictable and dynamic phenomena.
Chaotic systems often produce fractals. Take the famous Mandelbrot set, for example. This fractal is generated by a simple mathematical equation, but it reveals a mesmerizing world of swirling colors and intricate patterns. It’s like a cosmic Rorschach test that invites us to explore the infinite depths of chaos.
An introduction to chaotic dynamical systems devaney solutions is a fascinating topic that explores the behavior of complex systems over time. These systems can exhibit unpredictable and seemingly random behavior, making them challenging to understand. An error occurred in the underlying security system is an example of such a system, where the underlying mechanisms can be difficult to comprehend and control.
However, by studying chaotic dynamical systems devaney solutions, we can gain insights into the behavior of these complex systems and develop strategies for managing their unpredictability.
Conclusion
As we conclude our exploration of chaotic dynamical systems, we leave with a deep appreciation for their intricate nature and their profound implications across diverse fields. From cryptography to weather forecasting, the study of chaos has opened new avenues of understanding and innovation.
Devaney’s introduction to chaotic dynamical systems provides a roadmap to understanding complex phenomena. Just like an immune system trained to kill cancer can learn to recognize and eliminate threats, Devaney’s approach helps us decipher the patterns and dynamics that shape our world.
Yet, amidst the fascination, we acknowledge the challenges that accompany the harnessing of chaotic systems in real-world applications, underscoring the need for continued research and exploration in this captivating domain.
An introduction to chaotic dynamical systems devaney solutions, a branch of mathematics that studies complex systems and their unpredictable behaviors. These systems can be found in various real-world applications, like an ERP system, which is an information system based on a central database, managing data across multiple departments of an organization.
Coming back to chaotic dynamical systems, they’re characterized by their sensitivity to initial conditions, leading to unpredictable outcomes over time. Understanding these systems is crucial for fields like meteorology and economics.
Detailed FAQs
What is the key characteristic of a chaotic dynamical system?
A chaotic dynamical system exhibits extreme sensitivity to initial conditions, known as the butterfly effect, where even minuscule changes can lead to drastically different outcomes over time.
How is Devaney’s definition of chaos used in practice?
Devaney’s definition provides a rigorous mathematical framework for identifying and classifying chaotic systems, enabling researchers to analyze their behavior and potential applications.
What is the connection between fractals and chaotic dynamical systems?
Fractals are geometric patterns that exhibit self-similarity at different scales. They often arise from chaotic dynamical systems, providing visual representations of their complex behavior.