An ideal mass spring system vibrating with simple sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. As we embark on this journey, we will unravel the intricate workings of this system, exploring its fundamental principles and uncovering the captivating dance it performs.
Prepare to be captivated as we delve into the depths of simple harmonic motion, unraveling its mathematical elegance and witnessing its manifestations in the world around us. Together, we will explore the energy that flows within this system, tracing its transformations and marveling at the conservation of energy that governs its every move.
An ideal mass spring system vibrating with simple harmonic motion can be used to model a variety of physical phenomena, from the motion of a guitar string to the oscillations of a pendulum. An ERP system is an information system based on a central database that collects data from various departments within an organization.
This data can then be used to generate reports, track inventory, and manage customer relationships. An ideal mass spring system vibrating with simple harmonic motion can also be used to model the behavior of an electrical circuit.
Ideal Mass Spring System: An Ideal Mass Spring System Vibrating With Simple
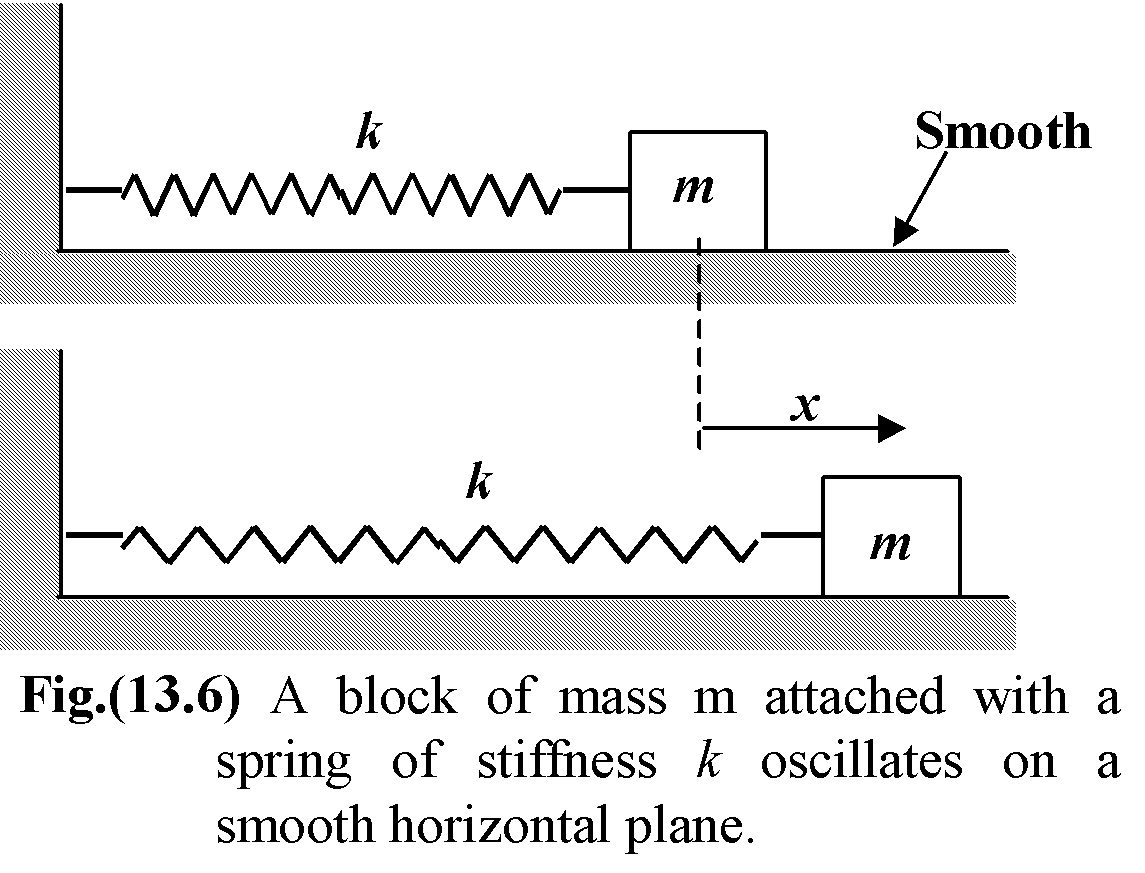
An ideal mass spring system consists of a mass attached to a spring. The mass is free to move back and forth along the spring. The spring exerts a restoring force on the mass, which is proportional to the displacement of the mass from its equilibrium position.
When an ideal mass spring system vibrates with simple harmonic motion, it’s like a well-oiled machine. But if you want to dive deeper into the nitty-gritty, check out an ess is an information system that supports the quizlet . It’s a treasure trove of knowledge for the curious minds.
Coming back to our mass spring system, its oscillations are a symphony of energy, a testament to the beauty of physics.
The ideal mass spring system is a simple model that can be used to study the behavior of real-world systems, such as pendulums and vibrating strings.
An ideal mass spring system vibrating with simple harmonic motion is a classic example of a system that can be controlled by an embedded system. An example of a real-time operating system that can be used to control such a system is the FreeRTOS operating system.
FreeRTOS is a free and open-source operating system that is designed for embedded systems. It is small, efficient, and easy to use, making it a good choice for controlling simple harmonic motion systems.
The diagram below shows an ideal mass spring system.

An ideal mass spring system vibrating with simple harmonic motion is like a yo-yo on a string. The mass goes up and down, up and down, just like the concentration of hydrogen and iodine in an equilibrium system for the reaction between hydrogen and iodine . But in that system, the concentrations don’t just go up and down, they reach a balance, just like the yo-yo eventually stops swinging.
The following assumptions are made in an ideal mass spring system:
- The mass is a point mass.
- The spring is massless and has no damping.
- The system is frictionless.
Simple Harmonic Motion
Simple harmonic motion is a periodic motion in which the restoring force is proportional to the displacement of the mass from its equilibrium position. The equation for simple harmonic motion is:
$$x = A\cos(\omega t + \phi)$$
where:
- $x$ is the displacement of the mass from its equilibrium position
- $A$ is the amplitude of the motion
- $\omega$ is the angular frequency of the motion
- $\phi$ is the phase angle of the motion
Examples of simple harmonic motion include the motion of a pendulum, the vibration of a guitar string, and the oscillation of a spring.
Energy in an Ideal Mass Spring System, An ideal mass spring system vibrating with simple
The total energy in an ideal mass spring system is the sum of the kinetic energy and the potential energy. The kinetic energy is the energy of the mass due to its motion, and the potential energy is the energy of the spring due to its deformation.
An ideal mass spring system vibrating with simple harmonic motion can provide valuable insights into the dynamics of real-world systems. Just as an erp system should be capable of integrating data from multiple sources , the mass spring system’s components work together seamlessly to create a stable and predictable oscillation.
By understanding the principles governing these systems, we can gain a deeper appreciation for the intricate workings of the universe and the technologies we rely on daily.
The equation for the total energy in an ideal mass spring system is:
$$E = \frac12kA^2$$
where:
- $E$ is the total energy
- $k$ is the spring constant
- $A$ is the amplitude of the motion
The conservation of energy in an ideal mass spring system states that the total energy of the system remains constant. This means that the kinetic energy and the potential energy can be converted into each other, but the total energy of the system remains the same.
Damping in an Ideal Mass Spring System
Damping is a force that opposes the motion of a mass spring system. Damping can be caused by friction, air resistance, or other factors. The effects of damping on an ideal mass spring system are to reduce the amplitude of the motion and to increase the period of the motion.
There are two types of damping:
- Viscous damping is a force that is proportional to the velocity of the mass.
- Coulomb damping is a force that is constant and opposes the motion of the mass.
Resonance in an Ideal Mass Spring System
Resonance is a phenomenon that occurs when the frequency of an external force matches the natural frequency of a mass spring system. When resonance occurs, the amplitude of the motion of the mass spring system increases dramatically.
The conditions for resonance are:
- The frequency of the external force must be equal to the natural frequency of the mass spring system.
- The damping in the system must be small.
The effects of resonance on an ideal mass spring system can be destructive. For example, resonance can cause bridges to collapse and buildings to sway. However, resonance can also be used to our advantage. For example, resonance is used in musical instruments to produce sound.
Last Recap
Our exploration of an ideal mass spring system vibrating with simple has illuminated the intricate interplay of physics and motion. We have witnessed the mesmerizing dance of simple harmonic motion, the harmonious exchange of energy, and the profound impact of damping and resonance.
An ideal mass spring system vibrating with simple harmonic motion is a great example of a system that can be used to illustrate the concepts of resonance and damping. The system can be used to demonstrate how the frequency of the driving force can affect the amplitude of the oscillations.
An example of a contractual vertical marketing system is a franchise agreement between a manufacturer and a retailer. In this type of agreement, the manufacturer grants the retailer the exclusive right to sell its products in a specific territory. The retailer agrees to meet certain standards set by the manufacturer, such as maintaining a certain level of inventory and providing customer service.
As we bid farewell to this captivating system, let us carry with us the lessons it has taught us about the rhythmic beauty of the physical world.
General Inquiries
What is an ideal mass spring system?
An ideal mass spring system vibrating with simple harmonic motion is a classic example of a damped harmonic oscillator. The system can be used to demonstrate the principles of resonance, damping, and energy dissipation. The system can also be used to design and build an example of an embedded system , such as a vibration sensor or a frequency generator.
The system can be used to study the effects of different damping mechanisms on the system’s response.
An ideal mass spring system is a theoretical model that represents a system consisting of a mass attached to a spring. The mass is assumed to be point-like, the spring is assumed to be massless and perfectly elastic, and the system is assumed to be frictionless and isolated from external influences.
Just like an ideal mass spring system vibrating with simple harmonic motion, the immune system responds to foreign invaders. However, an exaggerated response can lead to autoimmune disorders, where the immune system mistakenly attacks the body’s own tissues. Nevertheless, the ideal mass spring system remains a useful model for understanding the delicate balance of the immune system.
What is simple harmonic motion?
When an ideal mass spring system vibrates with simple harmonic motion, its displacement from equilibrium follows a sinusoidal function. This behavior is analogous to the flow of water in a lotic system, such as an example of lotic system . Just as the spring oscillates around its equilibrium position, the water in a lotic system flows in a predictable pattern, influenced by factors such as gravity and channel geometry.
Both systems exhibit periodic motion, highlighting the interconnectedness of physical phenomena.
Simple harmonic motion is a periodic motion in which the restoring force is directly proportional to the displacement from the equilibrium position and acts in the opposite direction. This type of motion is commonly observed in systems such as mass-spring systems, pendulums, and oscillating circuits.
How is energy conserved in an ideal mass spring system?
In an ideal mass spring system, the total mechanical energy (the sum of kinetic and potential energy) is conserved. This means that the total energy of the system remains constant throughout its motion, even though the kinetic and potential energies may be interconverted.
What is damping?
Damping is a force that opposes the motion of a system. In an ideal mass spring system, damping can be caused by factors such as air resistance or internal friction within the spring. Damping reduces the amplitude of the system’s oscillations over time.
What is resonance?
Resonance occurs when the frequency of an applied force matches the natural frequency of a system. At resonance, the amplitude of the system’s oscillations is greatly amplified. Resonance can be both beneficial (e.g., in tuning musical instruments) and detrimental (e.g.,
in causing bridges to collapse).